常用规划算法解析3-凸优化篇

前面两篇文章提到了前端优化中最常用到的两类规划算法——基于图搜索和基于采样。而前端规划给出的路径往往都是比较曲折的，即便考虑了车辆动力学约束的前端规划，也无法给出适合控制模块直接跟踪并满足舒适条件的路径。这也是为什么要引入后端轨迹优化的原因。后端轨迹优化后的路径有以下优点：

1. 更适合控制模块直接进行跟踪，并且容易达到较好的舒适效果
2. 更能节省耗能，避免了无效的能量浪费
3. 时间利用率上往往也能得到很大的提升

基于以上这些优点，我们可以看出为什么后端轨迹优化是如此重要的原因。而其中，在轨迹优化里运用最广泛的算法就是基于凸优化的方法，这篇文章就想和大家详细解读下基于凸优化的轨迹优化生成。

凸优化问题（convex optimization problem）指定义在凸集中的凸函数最优化的问题。尽管凸优化的条件比较苛刻，但经常应用于机器学习、自动驾驶规划等领域。

凸函数及凸集的定义如下所示：

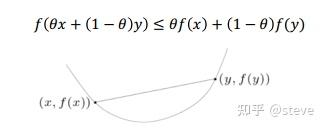
凸优化问题的优势主要有以下三点：

1. 凸优化问题的局部最优解就是全局最优解
2. 很多非凸问题都可以被等价转化为凸优化问题或者被近似为凸优化问题
3. 凸优化问题的研究较为成熟，当一个具体被归为一个凸优化问题，基本可以确定该问题是可被求解的

凸优化问题的求解已经很成熟，后面会推荐多个求解器。而在规划问题中，比较困难的部分在于如何将实际的场景构造成一个凸优化的问题，由于凸优化问题的要求比较严苛，这也为我们构造这类问题提出了挑战。

首先，我们考虑一个最简单的BVP（Boundary Value Problem）问题，即限定了轨迹的初始点及目标点，构造出一条平滑的轨迹。

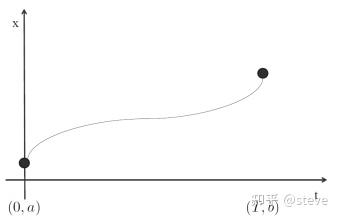
假设我们边界条件为起始点的（p,v,a）及目标点的（p,v,a），那么我们至少需要构造一个五阶多项式（包含6个系数）来进行连接才能够满足起止点的约束条件。

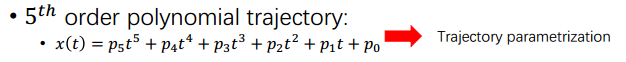
该问题的边界条件限制为：

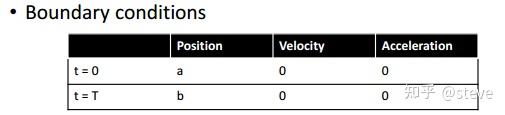
因此，该问题的求解可以简单地列出矩阵等式如下：

最简单的BVP问题是假设了时间一定的情况，其解是固定且唯一的。如果我们加入一个代价函数，这就变成了一个OBVP（Optimal Boundary Value Problem）问题，此时时间T就不是固定不变的，我们需要找到一个最优的T，使得代价函数的值最小。

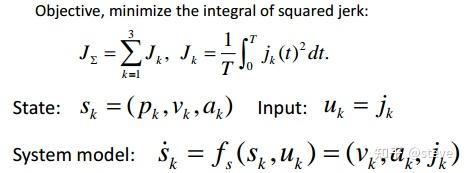
例如，我们设定代价函数只考虑Jerk的平方，状态空间为位置、速度、加速度，系统的输入为jerk值，然后再根据系统的模型来构造出状态转移方程。这样一个典型的OBVP问题也就构造好了。

求解上述OBVP问题需要用到庞特里亚金最小值原理，这里的数学推导比较复杂，本篇文章也就不赘述了，感兴趣的读者可以参考论文

ps. 该篇论文讲解很详细，很推荐读者去精读一下

最终可以推导出cost function只与T有关，公式如下所示：

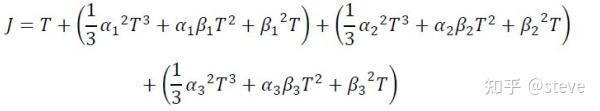
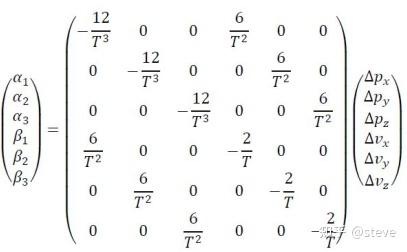
因此要使得cost function J最小，只需要对其求一阶导并令其为0即可，这里的求解方法有多种，可以利用伴随矩阵求特征值的方法，也可以利用Eigen内置的多项式求解器等等。最终可以求得最优的时间段T，使得这条轨迹的代价函数最小。需要注意的是，这里限制了目标点的v,a，这使得J只与时刻T相关而不与T时刻的v，a状态相关。关于不限制目标点v，a的OBVP问题读者感兴趣的话可以自行搜索。

做移动机器人的读者应该对frenet坐标系非常了解了，不同于笛卡尔坐标系，frenet坐标系作为一个动态坐标系更能很好的反映当前道路的实际情况，并且在此坐标系下，我们的路径规划问题从二维降成了一维，维度的下降使得优化速度得到显著提升。另外，基于frenet坐标系进行规划可以使得横纵向解耦开，这样在实际工程中更容易进行调试、发现问题。由于frenet坐标系的这些优势，在自动驾驶领域中已经成为了一个主流的规划方法，例如Apollo中进行轨迹优化时采用的就是该坐标系。

因此在frenet坐标系中进行路径规划的时候，我们只需要考虑横向的位置（即d值）即可，这样在一维空间中的规划效率就提高了很多。

最终的优化效果如下图所示，蓝色的线为道路中心线，红色的线为优化轨迹。

上面讲到一段轨迹的优化生成，即OBVP问题。在实际应用中，往往我们会给出多个waypoints，即途经点，我们需要规划出的轨迹能平滑的经过所有的途经点从而到达最终的目标点。这类问题其实就是单段OBVP问题的扩展，即多段轨迹优化问题（Multi-Segment Trajectory Generation）。

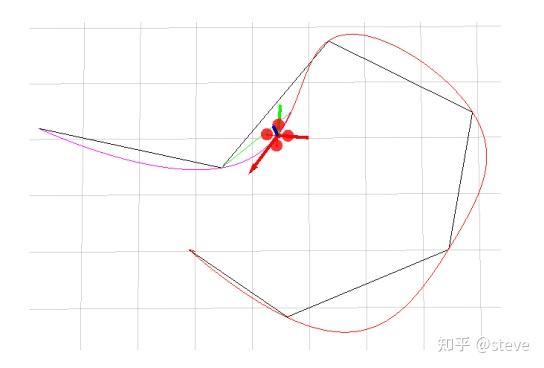
构建多段轨迹优化问题，我们可以将每一段都看做一个BVP问题，用一个多项式去连接它们，然后再进行每段之间的连续性约束，即相邻两段多项式的首尾状态要相等。接下来介绍基于该思想的minimum snap算法。

Minimum Snap算法，即最小化运动状态中的snap值，snap即jerk的导数，在无人机中这个量表示差动推力（differential thrust），最小化snap量也就是最省能量，能源利用率最高。在该算法中，首先我们构建每一段的多项式参数化方程：

由于我们的状态量为[p, v, a, j]四个值，那么每一段轨迹就含有8个未知数，因此需要7阶多项式来进行连接。这里需要说明的是，除了首尾两个端点为强约束外，中间的middle waypoints的状态量（[v, a, j]）其实是优化得出的，但我们这里使用7阶多项式其实是为了应对没有middle waypoints的情况，也就是只有首尾端点的话（8个未知数）至少是需要7阶多项式才能满足的，因此为了方便起见，我们将每段都统一成7阶多项式，读者在构建自己的算法时，可以依照实际情况进行多项式的阶数选择。

构建完了参数化方程，接下来的代价函数就很容易，Minimum Snap算法的代价函数自然是snap值的平方，即每段多项式的四阶导平方再求和。

约束条件上面已简单提到过，这边总结一下，约束条件主要有以下几个：

1. 首尾端点的状态量约束
2. middle waypoints的p值约束

3. 相邻两段多项式之间的连续性约束（即相邻两段多项式的首尾端点的状态量要相等）

最终将代价函数与约束条件连列就得到了一个QP（Quadratic Programming）问题：

QP问题，即代价函数为二次函数，是最简单的一种凸优化问题，当我们将规划问题转变成二次优化问题时，便有很多种求解器可以供我们选择进行问题求解了。

从上面的Minimum Snap问题构造我们可以看出，该二次优化问题只包含了等式约束，对于这类问题我们可以将等式约束带入进代价函数中，从而使问题转变为一个不受约束的二次优化问题，这样我们就可以进行闭式求解了。

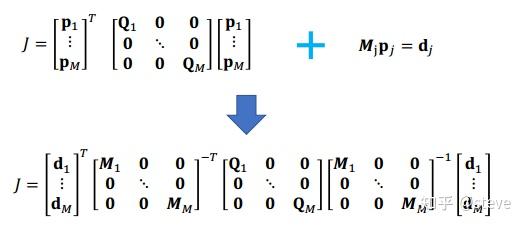
这里我们需要用到一个选择矩阵C来区分无约束的变量（dp）和受约束的变量（df），最终可以进行闭式求解的形式如下所示：

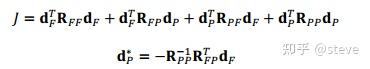
与迭代求解法不同，闭式求解法直接会给出一个最终解，但由于里面牵涉到矩阵取逆的操作，在变量过多的时候，效率会非常低。因此一般情况下还是推荐大家使用QP求解器进行求解。

1. CVX

Matlab中的一款凸优化求解器，比较好用轻量级。

2. Mosek

非常鲁棒的一款凸优化求解器，可以求解几乎所有的凸优化问题，但只有x86版本的库提供，想应用在嵌入式arm设备上目前还没有开放版本。

3. OOQP

开源的一款求解二次优化问题的求解器

4. GLPK

开源的一款求解线性问题的求解器

5. OSQP

我个人用的比较多的二次优化求解器，速度非常快，也比较鲁棒

以上就介绍完了基于凸优化的规划算法。这类算法应该是自动驾驶规划领域应用比较多的一类算法，我平时在工作中也经常会使用。该类算法的速度非常快，也能给出全局最优解，并且能很好地将障碍物、交规、地图信息等等通过约束的形式构建出来，非常直观鲁棒。我也推荐大家可以多关注一下这类算法，同时对文章有任何的问题与建议，也非常欢迎在评论区留言~